

In the expression 2x + 3, the coefficient of x is the number 2, and it means 2 times x plus 3. Firstly, when students are entering expressions with complex syntax into a CAS they need to be able to recognise whether the expression entered is equivalent to.
#Equivalent expressions how to#
All variables must have a coefficient, a number that is multiplied by the variable. Learn how to make equivalent expressions using the Commutative and Associative properties, how to handle pesky subtraction and division, and how to identify. This math operation can be addition, subtraction, multiplication, and division.Īn example of a mathematical expression with a variable is 2x + 3. Examples of operation symbols are the ones for addition, subtraction, multiplication, and division.Īlso to know is, what is a defined expression?Īn expression is a sentence with a minimum of two numbers and at least one math operation. A numerical expression is a mathematical sentence involving only numbers and one or more operation symbols. Equivalent Expressions Skill Objective: EQUIVALENT EXPRESSIONS The student will know how to find an equivalent expression to the given expression by solving each expression and finding the expressions that are equal by completing multiple choice questions. Likewise, what is a numerical expression? Numerical Expression Definition. Then, what is an example of an equivalent expression?Įxamples of Equivalent Expressions 3x+2 and 3x + 6 are equivalent expressions, because the value of both the expressions remains same for any value of x. For example, students would have to match that 2 + 5x + 3y + x + y is equal to 2(3x + 2y + 1). If you plug in the same variable value into equivalent expressions, they will each give you the same value when you simplify. A fun and different way of getting your students to practice identifying equivalent expressions This activity gets your students matching and simplifying equivalent expressions. Equivalent expressions are expressions that are the same, even though they may look a little different. Would it be possible for a symmetric axial vector torque to be equivalent to the shear stress of two uniform rectilinear forces as they seem to be non-related, but it works out that they should be. Which of the following expressions is equivalent to (AB)C 1. Prerequisite: Write and Evaluate Expressions with. Students need to be able to explain that the expression $(2x+3)(5x+4)$ is equivalent to $10x^\approx 2.54575\cdots$) to a specified place.If two things are equivalent, they are the same. Equivalent expressions Thread starter rae20 Start date 1 rae20. Vocabulary evaluate to find the value of an algebraic expression. Instruction at the high school should highlight these properties as students begin to work with polynomials. Instruction at the elementary and middle school levels should pay explicit attention to these properties and how they are used to generate equivalent expressions. Students who calculate the value of the expression $4\times 7\times 25$ by first multiplying the $4$ and the $25$ to get $100$ then multiply this result by $7$ are using the associative and commutative properties of multiplication to generate equivalent expressions. Students who calculate $6\times 8$ by thinking of the problem as $5\times 8+8$ are using the distributive property to reason that both expressions are equivalent. Number of Unique Solutions: 26 1: 2(3x +. If two algebraic expressions are equivalent, then the two expressions have the same value when we plug in the same value (s) for the variable (s). Directions: Using the digits 1 to 9 at most one time each, fill in the boxes to create two equivalent expressions. In elementary school students learn multiplication facts by building on facts that they already know. Equivalent expressions are expressions that work the same even though they look different.
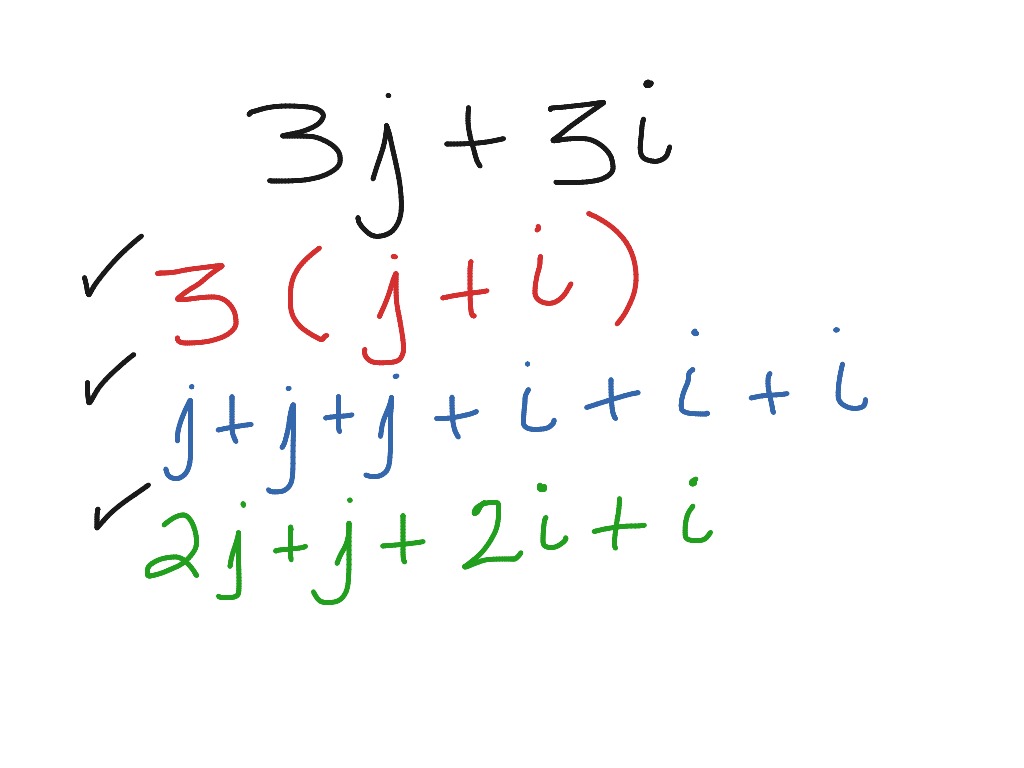
But in reality, the expressions are equivalent, just written a different way.

This is an important distinction, because often, students think that they are changing an expression to something else. Generating equivalent expressions and giving reasons as to why two expressions are equivalent provides a cornerstone for making sense of the structure of algebraic expressions. Then, students glue them on their answer sheet to show that the expressions are equivalent to each other. Instructional IEP learning goal in Math, Expressions and Equations for students in grade 6 about Creating Equivalent Expressions and aligned to AAS.6.EE.


 0 kommentar(er)
0 kommentar(er)
